Construction of t-norms
In mathematics, t-norms are a special kind of binary operations on the real unit interval [0, 1]. Various constructions of t-norms, either by explicit definition or by transformation from previously known functions, provide a plenitude of examples and classes of t-norms. This is important, e.g., for finding counter-examples or supplying t-norms with particular properties for use in engineering applications of fuzzy logic. The main ways of construction of t-norms include using generators, defining parametric classes of t-norms, rotations, or ordinal sums of t-norms.
Relevant background can be found in the article on t-norms.
Contents |
Generators of t-norms
The method of constructing t-norms by generators consists in using a unary function (generator) to transform some known binary function (most often, addition or multiplication) into a t-norm.
In order to allow using non-bijective generators, which do not have the inverse function, the following notion of pseudo-inverse function is employed:
- Let f: [a, b] → [c, d] be a monotone function between two closed subintervals of extended real line. The pseudo-inverse function to f is the function f (−1): [c, d] → [a, b] defined as
Additive generators
The construction of t-norms by additive generators is based on the following theorem:
- Let f: [0, 1] → [0, +∞] be a strictly decreasing function such that f(1) = 0 and f(x) + f(y) is in the range of f or equal to f(0+) or +∞ for all x, y in [0, 1]. Then the function T: [0, 1]2 → [0, 1] defined as
- T(x, y) = f (-1)(f(x) + f(y))
- is a t-norm.
If a t-norm T results from the latter construction by a function f which is right-continuous in 0, then f is called an additive generator of T.
Examples:
- The function f(x) = 1 – x for x in [0, 1] is an additive generator of the Łukasiewicz t-norm.
- The function f defined as f(x) = –log(x) if 0 < x ≤ 1 and f(0) = +∞ is an additive generator of the product t-norm.
- The function f defined as f(x) = 2 – x if 0 ≤ x < 1 and f(1) = 0 is an additive generator of the drastic t-norm.
Basic properties of additive generators are summarized by the following theorem:
- Let f: [0, 1] → [0, +∞] be an additive generator of a t-norm T. Then:
- T is an Archimedean t-norm.
- T is continuous if and only if f is continuous.
- T is strictly monotone if and only if f(0) = +∞.
- Each element of (0, 1) is a nilpotent element of T if and only if f(0) < +∞.
- The multiple of f by a positive constant is also an additive generator of T.
- T has no non-trivial idempotents. (Consequently, e.g., the minimum t-norm has no additive generator.)
Multiplicative generators
The isomorphism between addition on [0, +∞] and multiplication on [0, 1] by the logarithm and the exponential function allow two-way transformations between additive and multiplicative generators of a t-norm. If f is an additive generator of a t-norm T, then the function h: [0, 1] → [0, 1] defined as h(x) = e−f (x) is a multiplicative generator of T, that is, a function h such that
- h is strictly increasing
- h(1) = 1
- h(x) · h(y) is in the range of h or equal to 0 or h(0+) for all x, y in [0, 1]
- h is right-continuous in 0
- T(x, y) = h (−1)(h(x) · h(y)).
Vice versa, if h is a multiplicative generator of T, then f: [0, 1] → [0, +∞] defined by f(x) = −log(h(x)) is an additive generator of T.
Parametric classes of t-norms
Many families of related t-norms can be defined by an explicit formula depending on a parameter p. This section lists the best known parameterized families of t-norms. The following definitions will be used in the list:
- A family of t-norms Tp parameterized by p is increasing if Tp(x, y) ≤ Tq(x, y) for all x, y in [0, 1] whenever p ≤ q (similarly for decreasing and strictly increasing or decreasing).
- A family of t-norms Tp is continuous with respect to the parameter p if
-
- for all values p0 of the parameter.
Schweizer–Sklar t-norms
The family of Schweizer–Sklar t-norms, introduced by Berthold Schweizer and Abe Sklar in the early 1960s, is given by the parametric definition
A Schweizer–Sklar t-norm 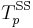 is
is
- Archimedean if and only if p > −∞
- Continuous if and only if p < +∞
- Strict if and only if −∞ < p ≤ 0 (for p = −1 it is the Hamacher product)
- Nilpotent if and only if 0 < p < +∞ (for p = 1 it is the Łukasiewicz t-norm).
The family is strictly decreasing for p ≥ 0 and continuous with respect to p in [−∞, +∞]. An additive generator for 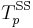 for −∞ < p < +∞ is
for −∞ < p < +∞ is
Hamacher t-norms
The family of Hamacher t-norms, introduced by Horst Hamacher in the late 1970s, is given by the following parametric definition for 0 ≤ p ≤ +∞:
The t-norm 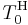 is called the Hamacher product.
is called the Hamacher product.
Hamacher t-norms are the only t-norms which are rational functions. The Hamacher t-norm 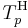 is strict if and only if p < +∞ (for p = 1 it is the product t-norm). The family is strictly decreasing and continuous with respect to p. An additive generator of
is strict if and only if p < +∞ (for p = 1 it is the product t-norm). The family is strictly decreasing and continuous with respect to p. An additive generator of 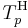 for p < +∞ is
for p < +∞ is
Frank t-norms
The family of Frank t-norms, introduced by M.J. Frank in the late 1970s, is given by the parametric definition for 0 ≤ p ≤ +∞ as follows:
The Frank t-norm 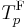 is strict if p < +∞. The family is strictly decreasing and continuous with respect to p. An additive generator for
is strict if p < +∞. The family is strictly decreasing and continuous with respect to p. An additive generator for 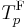 is
is
Yager t-norms
The family of Yager t-norms, introduced in the early 1980s by Ronald R. Yager, is given for 0 ≤ p ≤ +∞ by
The Yager t-norm 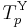 is nilpotent if and only if 0 < p < +∞ (for p = 1 it is the Łukasiewicz t-norm). The family is strictly increasing and continuous with respect to p. The Yager t-norm
is nilpotent if and only if 0 < p < +∞ (for p = 1 it is the Łukasiewicz t-norm). The family is strictly increasing and continuous with respect to p. The Yager t-norm 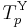 for 0 < p < +∞ arises from the Łukasiewicz t-norm by raising its additive generator to the power of p. An additive generator of
for 0 < p < +∞ arises from the Łukasiewicz t-norm by raising its additive generator to the power of p. An additive generator of 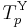 for 0 < p < +∞ is
for 0 < p < +∞ is
Aczél–Alsina t-norms
The family of Aczél–Alsina t-norms, introduced in the early 1980s by János Aczél and Claudi Alsina, is given for 0 ≤ p ≤ +∞ by
The Aczél–Alsina t-norm 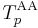 is strict if and only if 0 < p < +∞ (for p = 1 it is the product t-norm). The family is strictly increasing and continuous with respect to p. The Aczél–Alsina t-norm
is strict if and only if 0 < p < +∞ (for p = 1 it is the product t-norm). The family is strictly increasing and continuous with respect to p. The Aczél–Alsina t-norm 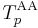 for 0 < p < +∞ arises from the product t-norm by raising its additive generator to the power of p. An additive generator of
for 0 < p < +∞ arises from the product t-norm by raising its additive generator to the power of p. An additive generator of 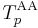 for 0 < p < +∞ is
for 0 < p < +∞ is
Dombi t-norms
The family of Dombi t-norms, introduced by József Dombi (1982), is given for 0 ≤ p ≤ +∞ by
The Dombi t-norm 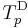 is strict if and only if 0 < p < +∞ (for p = 1 it is the Hamacher product). The family is strictly increasing and continuous with respect to p. The Dombi t-norm
is strict if and only if 0 < p < +∞ (for p = 1 it is the Hamacher product). The family is strictly increasing and continuous with respect to p. The Dombi t-norm 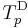 for 0 < p < +∞ arises from the Hamacher product t-norm by raising its additive generator to the power of p. An additive generator of
for 0 < p < +∞ arises from the Hamacher product t-norm by raising its additive generator to the power of p. An additive generator of 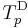 for 0 < p < +∞ is
for 0 < p < +∞ is
Sugeno–Weber t-norms
The family of Sugeno–Weber t-norms was introduced in the early 1980s by Siegfried Weber; the dual t-conorms were defined already in the early 1970s by Michio Sugeno. It is given for −1 ≤ p ≤ +∞ by
The Sugeno–Weber t-norm 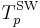 is nilpotent if and only if −1 < p < +∞ (for p = 0 it is the Łukasiewicz t-norm). The family is strictly increasing and continuous with respect to p. An additive generator of
is nilpotent if and only if −1 < p < +∞ (for p = 0 it is the Łukasiewicz t-norm). The family is strictly increasing and continuous with respect to p. An additive generator of 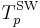 for 0 < p < +∞ [sic] is
for 0 < p < +∞ [sic] is
Ordinal sums
The ordinal sum constructs a t-norm from a family of t-norms, by shrinking them into disjoint subintervals of the interval [0, 1] and completing the t-norm by using the minimum on the rest of the unit square. It is based on the following theorem:
- Let Ti for i in an index set I be a family of t-norms and (ai, bi) a family of pairwise disjoint (non-empty) open subintervals of [0, 1]. Then the function T: [0, 1]2 → [0, 1] defined as
- is a t-norm.
The resulting t-norm is called the ordinal sum of the summands (Ti, ai, bi) for i in I, denoted by
or  if I is finite.
if I is finite.
Ordinal sums of t-norms enjoy the following properties:
- Each t-norm is a trivial ordinal sum of itself on the whole interval [0, 1].
- The empty ordinal sum (for the empty index set) yields the minimum t-norm Tmin. Summands with the minimum t-norm can arbitrarily be added or omitted without changing the resulting t-norm.
- It can be assumed without loss of generality that the index set is countable, since the real line can only contain at most countably many disjoint subintervals.
- An ordinal sum of t-norm is continuous if and only if each summand is a continuous t-norm. (Analogously for left-continuity.)
- An ordinal sum is Archimedean if and only if it is a trivial sum of one Archimedean t-norm on the whole unit interval.
- An ordinal sum has zero divisors if and only if for some index i, ai = 0 and Ti has zero divisors. (Analogously for nilpotent elements.)
If 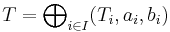 is a left-continuous t-norm, then its residuum R is given as follows:
is a left-continuous t-norm, then its residuum R is given as follows:
where Ri is the residuum of Ti, for each i in I.
Ordinal sums of continuous t-norms
The ordinal sum of a family of continuous t-norms is a continuous t-norm. By the Mostert–Shields theorem, every continuous t-norm is expressible as the ordinal sum of Archimedean continuous t-norms. Since the latter are either nilpotent (and then isomorphic to the Łukasiewicz t-norm) or strict (then isomorphic to the product t-norm), each continuous t-norm is isomorphic to the ordinal sum of Łukasiewicz and product t-norms.
Important examples of ordinal sums of continuous t-norms are the following ones:
- Dubois–Prade t-norms, introduced by Didier Dubois and Henri Prade in the early 1980s, are the ordinal sums of the product t-norm on [0, p] for a parameter p in [0, 1] and the (default) minimum t-norm on the rest of the unit interval. The family of Dubois–Prade t-norms is decreasing and continuous with respect to p..
- Mayor–Torrens t-norms, introduced by Gaspar Mayor and Joan Torrens in the early 1990s, are the ordinal sums of the Łukasiewicz t-norm on [0, p] for a parameter p in [0, 1] and the (default) minimum t-norm on the rest of the unit interval. The family of Mayor–Torrens t-norms is decreasing and continuous with respect to p..
Rotations
The construction of t-norms by rotation was introduced by Sándor Jenei (2000). It is based on the following theorem:
- Let T be a left-continuous t-norm without zero divisors, N: [0, 1] → [0, 1] the function that assigns 1 − x to x and t = 0.5. Let T1 be the linear transformation of T into [t, 1] and
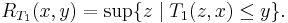 Then the function
Then the function
- is a left-continuous t-norm, called the rotation of the t-norm T.
Geometrically, the construction can be described as first shrinking the t-norm T to the interval [0.5, 1] and then rotating it by the angle 2π/3 in both directions around the line connecting the points (0, 0, 1) and (1, 1, 0).
The theorem can be generalized by taking for N any strong negation, that is, an involutive strictly decreasing continuous function on [0, 1], and for t taking the unique fixed point of N.
The resulting t-norm enjoys the following rotation invariance property with respect to N:
- T(x, y) ≤ z if and only if T(y, N(z)) ≤ N(x) for all x, y, z in [0, 1].
The negation induced by Trot is the function N, that is, N(x) = Rrot(x, 0) for all x, where Rrot is the residuum of Trot.
See also
References
- Klement, Erich Peter; Mesiar, Radko; and Pap, Endre (2000), Triangular Norms. Dordrecht: Kluwer. ISBN 0-7923-6416-3.
- Fodor, János (2004), "Left-continuous t-norms in fuzzy logic: An overview". Acta Polytechnica Hungarica 1(2), ISSN 1785-8860 [1]
- Dombi, József (1982), "A general class of fuzzy operators, the DeMorgan class of fuzzy operators and fuzziness measures induced by fuzzy operators". Fuzzy Sets and Systems 8, 149–163.
- Jenei, Sándor (2000), "Structure of left-continuous t-norms with strong induced negations. (I) Rotation construction". Journal of Applied Non-Classical Logics 10, 83–92.
- Mirko Navara (2007), "Triangular norms and conorms", Scholarpedia [2].
![f^{(-1)}(y) = \begin{cases}
\sup \{ x\in[a,b] \mid f(x) < y \} & \mbox{for } f \mbox{ non-decreasing} \\
\sup \{ x\in[a,b] \mid f(x) > y \} & \mbox{for } f \mbox{ non-increasing.}
\end{cases}](/2012-wikipedia_en_all_nopic_01_2012/I/105e6bc2ea25a206f0484d1cd23d65b9.png)
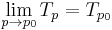
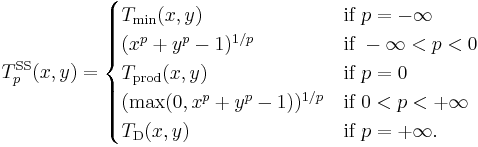
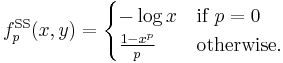
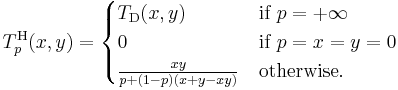
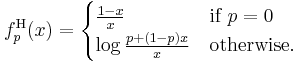
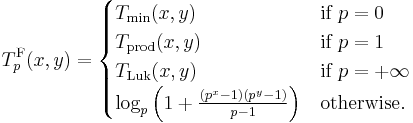
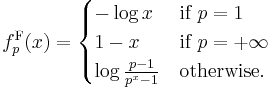
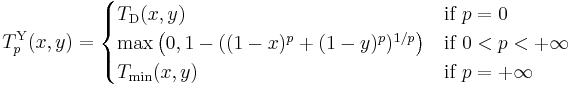
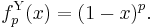
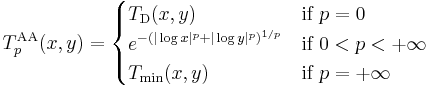
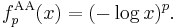
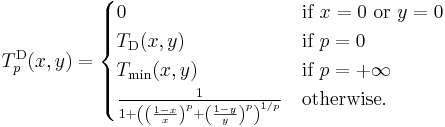
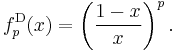
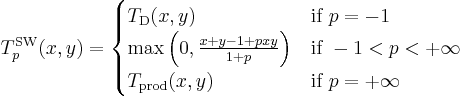
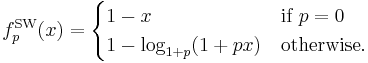
![T(x, y) = \begin{cases}
a_i %2B (b_i - a_i) \cdot T_i\left(\frac{x - a_i}{b_i - a_i}, \frac{y - a_i}{b_i - a_i}\right)
& \mbox{if } x, y \in [a_i, b_i]^2 \\
\min(x, y) & \mbox{otherwise}
\end{cases}](/2012-wikipedia_en_all_nopic_01_2012/I/9376ea24e55d11a125cf81967f99150b.png)
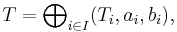
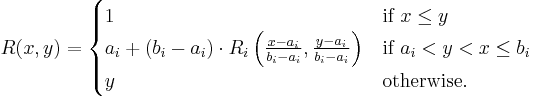
![T_{\mathrm{rot}} = \begin{cases}
T_1(x, y) & \mbox{if } x, y \in (t, 1] \\
N(R_{T_1}(x, N(y))) & \mbox{if } x \in (t, 1] \mbox{ and } y \in [0, t] \\
N(R_{T_1}(y, N(x))) & \mbox{if } x \in [0, t] \mbox{ and } y \in (t, 1] \\
0 & \mbox{if } x, y \in [0, t]
\end{cases}](/2012-wikipedia_en_all_nopic_01_2012/I/33ae5148ca39d31bfcf88134ce3b9a92.png)